How to square a square? How can you devide a square into smaller DIFFERENT squares?
Seems simple. We had seen an old 175 x 175 solution found in 1956 ... but still it took us 15 years to find the first few ourselves.

While working on imperfect squares we expected to find the perfect ones automatically. Via the perfect rectangles we found them earlier, that algorithm is more efficient for this purpose. Hard to believe that there will exist probably infinite solutions! The 110-square is the smallest known, but not proven yet to be the smallest possible. We are quite certain that the smallest possible is at least 110x110, Unfortunately our algorithm is still much too slow for the larger puzzles.

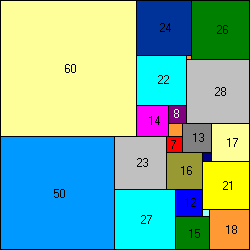110x110 puzzle, 22 squares.
Working with a large square (60x60) we didn't expect to find a perfect solution. We found two!

110x110 puzzle, also 22 squares.
Very simular to the first one.

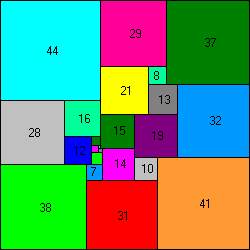110x110 puzzle, with 23 squares.


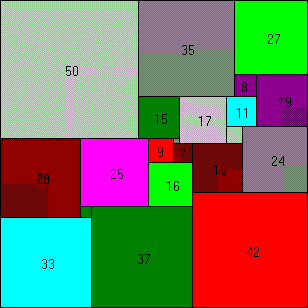112x112 puzzel, with 21 squares.

Mathematicians proved that a solution should exist of at least 21 squares (with only one solution). All other solutions will have 22+ squares.

Links:

squaring.net. Thousants perfect squares and rectangles!
Mathworld - Perfect Square Dissection